Rigidezza molla

La rigidezza è la capacità che ha un corpo di opporsi alla deformazione elastica provocata da una forza applicata. In generale si dovrebbe usare il termine rigidezza quando si parla di una struttura, di rigidità quando si parla di un materiale. Problematiche progettuali: tipo di molla da impiegare posizionamento nel cinematismo di azionamento scelta del materiale tecnologia di produzione ifi d ll.

Programma per calcolare la rigidita delle molle. DIAGRAMMA CARICO-FRECCIA.

Nel caso di molle accoppiate in serie o in parallelo la rigidezza del sistema è. Sto cercando un mono usato su internet. Vorrei sapere come si interpretano le tabelle riguardanti la rigidezza delle molle. Vi faccio un esempio con questa tabella che ho trovato: Link a pagina di Imageshack. Queste tabelle permettono di operare la conversione dei valori di rigidezza delle molle , nelle unità di misura più usate sulle autovetture da competizione. Una carrozza ferroviaria di massa M appoggia su carrelli, mediante molle ad elica cilindrica a sezione circolare per ogni carrello.

Basandosi sulla teoria elementare per il calcolo di queste molle (vedi figura):.

Riduzione o esaltazione delle vibrazioni. Comando di organi in movimento. Immagazzinamento di energia. Applicazione di forze proporzionali.

In base al tipo di sollecitazione cui sono soggette si hanno molle di flessione, molle di torsione e molle di trazione e compressione. Se una forza esterna F agisce su una molla , questa subisce una accorciamento f. Il comportamento della gomma però non è lineare perché la deformazione non è direttamente proporzionale alla forza applicata. Quindi per la gomma non è valida la legge di Hooke.

Sono elementi finiti monodimensionali costituiti da due nodi di estremità. I risultati che si possono ottenere da elementi di tipo. SPRING sono le forze o gli spostamenti nodali. Consentono di riprodurre il comportamento di molle lineari attraverso la nota relazione: F=Ku. Quando lo spostamento , anche la molla k bilxx II entra in funzione, e la nuova rigidezza (2° stadio) è quella complessiva del sistema di molle in serie.

Se un materiale presenta un comportamento elastico in corrispondenza di un . Modelli lineari di molle elastiche. La rigidezza può essere costante o variabile, cioè la freccia può avere rispettivamente un andamento lineare o non .

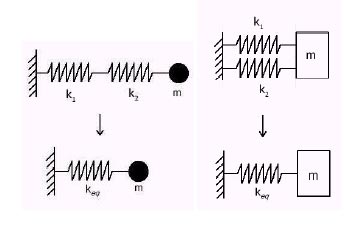
Espressa tale rigidezza di 2° stadio, in funzione della rigidezza kt della la molla componente, k =a-kt (con 0orl), essa è facilmente esprimibile anche in funzione .